
Finite symmetry Finite dim QEC codes Continuous symmetry Infinite dim QEC codes Construct high quality symmetric quantum codes. Study approximate QEC! Prove strong upper bounds on the quality of these codes.
#Approximate quantum error correction code#
There is no exact finite dim QEC code with continuous symmetry. Infinite dim codes for continuous symmetries.
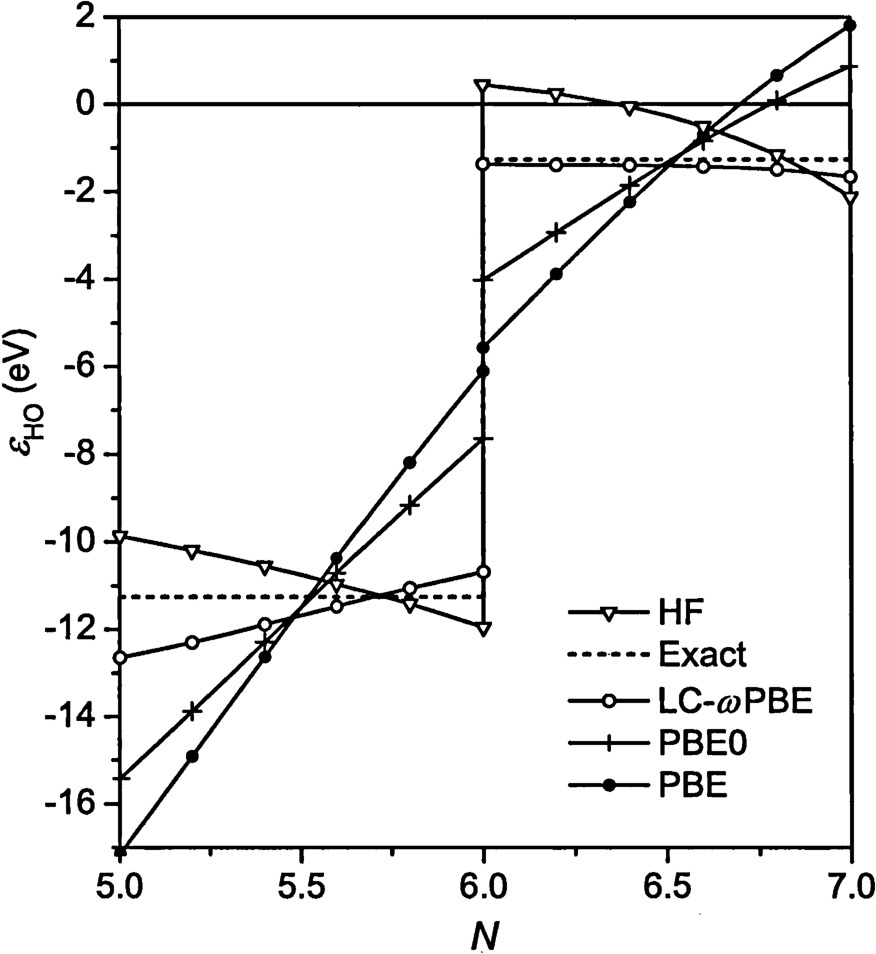
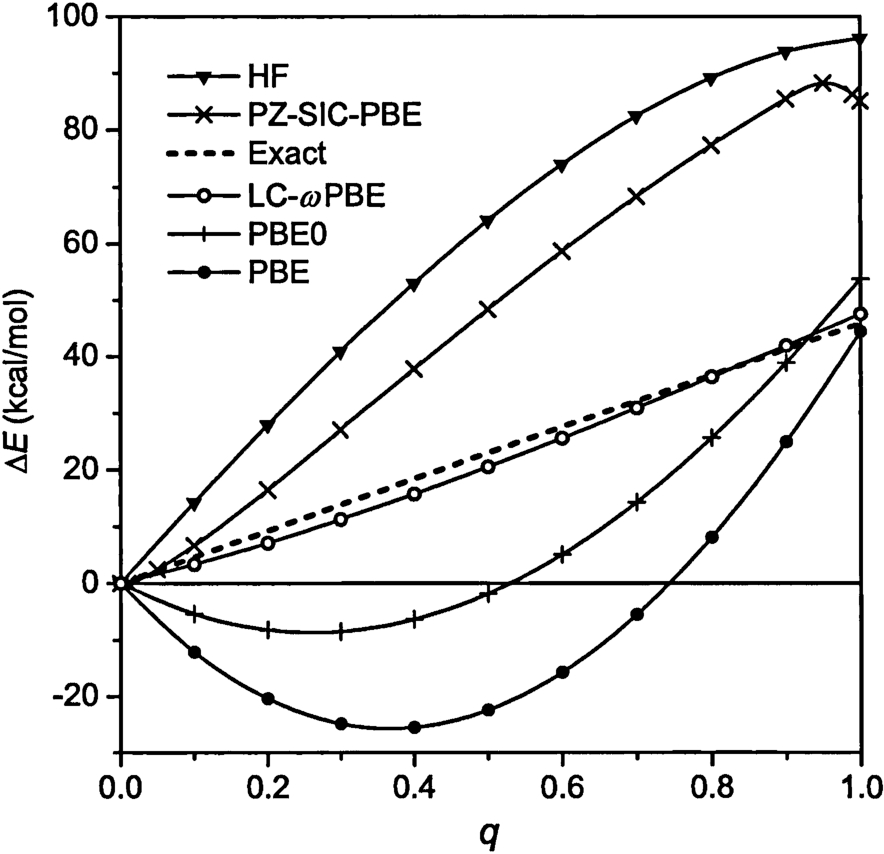
Finite symmetry Finite dim QEC codes Dimension of local subsystem = size of the symmetry group Continuous symmetry Infinite dim QEC codes Sometimes not normalizable…ġ7 Take home message We can construct exact erasure correcting codes: Finite dim codes for finite symmetries. We can construct codes on regular representation of any group. Take home message We can construct exact erasure correcting codes: Finite dim codes for finite symmetries. Finite symmetry Finite dim QEC codes Continuous symmetry Infinite dim QEC codesġ6 We can construct codes on regular representation of any group. We can construct exact erasure correcting codes: Finite dim codes for finite symmetries. Encoding Encoding … … Logical Physical Logical Physical Eastin & Knill: There is no code with 1 & 2!ġ4 Take home message Finite symmetry Finite dim QEC codes Continuousġ5 Take home message Finite symmetry Finite dim QEC codes Continuous Approximate Eastin-Knill Eastin & Knill: There is no QEC code with a continuous symmetry. Approximate quantum error correction Study: 2. Transversally implement universal logical gates (by a tensor product operator): We do not necessarily need perfect codes! 1. Approximate Eastin-KnillĮastin-Knill theorem Ideally we want to: Correct erasure of a single subsystem. Encoding Encoding … … Logical Physical Logical Physical Eastin & Knill: There is no code with 1 & 2!ġ2 1. Transversally implement universal logical gates (by a tensor product operator): Eastin & Knill: There is no QEC code with a continuous symmetry. Transversally implement universal logical gates (by a tensor product operator): Encoding Encoding … … Logical Physical Logical Physical Eastin & Knill: There is no code with 1 & 2!ġ1 Eastin-Knill theorem Ideally we want to: Correct erasure of a single subsystem. Entanglement wedge of CFT subsystem A: the region in the bulk enclosed by A, and ˠA, the minimal surface in the bulk with same boundaries as A: Entanglement wedge reconstruction: any operator in the entanglement wedge of A has a dual on A => QEC! Logical A1 A2 A3 Time Symmetry: Time translationġ0 Eastin & Knill: There is no code with 1 & 2!Įastin-Knill theorem Ideally we want to: Correct erasure of a single subsystem. Holographic duality AdS/CFT correspondence: bulk quantum gravity boundary CFT. Entanglement wedge of CFT subsystem A: the region in the bulk enclosed by A, and ˠA, the minimal surface in the bulk with same boundaries as A: Entanglement wedge reconstruction: any operator in the entanglement wedge of A has a dual on A => QEC! A1 A2 A3 ˠ A1A2 A3A2 A1A3 Fixed time slice d+1 quantum gravity: Bulk theory Boundary theory d CFT: ˠA ˠ A Reference frame QEC Hayden et al., arXiv: Condensed matter systems Brandao et al., arXiv: Time Time A1 Holographic duality Logical Next slides Harlow et al., arXiv: A3 A2 Fault-tolerant quantum computation Next slides Eastin/Knill, PRL, 2009Ĩ Holographic duality AdS/CFT correspondence: bulk quantum gravity boundary CFT. Symmetry group: G g => representation: ui(g) Encoding Encoding … … Logical Physical Logical Physical Covariance: Rotate, then encode = Encode, then rotate Logical Physical This talk: only erasure correction of a single physical subsystem! There is a conflict between symmetry and QEC! Our goal is to formalize and understand this conflict. 1Stanford University, 2Caltech, 3Freie Universität Berlin I am Sepehr Nezami, a PhD student at Stanford and I'll be moving to Caltech to start my posdoc next year and this a joint work with my wonderful collaborators. Albert, Grant Salton, Fernando Pastawski, Patrick Hayden, John Preskill Today, I'm gonna present this work, Continuous symmetries and approximate quantum error correction, which is a joint collaboration between Caltech and Stanford that is supported through the supplement of MURI. 1 Continuous symmetries and approximate quantum error correctionĪrXiv: Sepehr Nezami Stanford University Philippe Faist, Victor V.


 0 kommentar(er)
0 kommentar(er)
